0、哈密顿算子∇
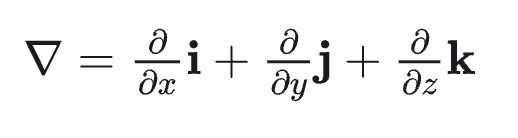
1、梯度(Gradient)是矢量,也是法向量
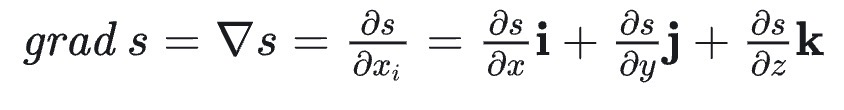
2、散度(Divergence)是标量
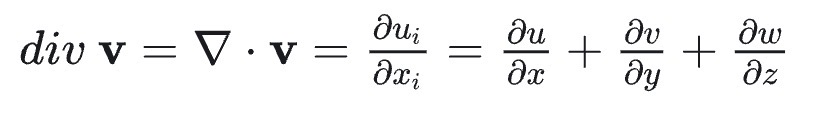
3、旋度(Curl)是向量
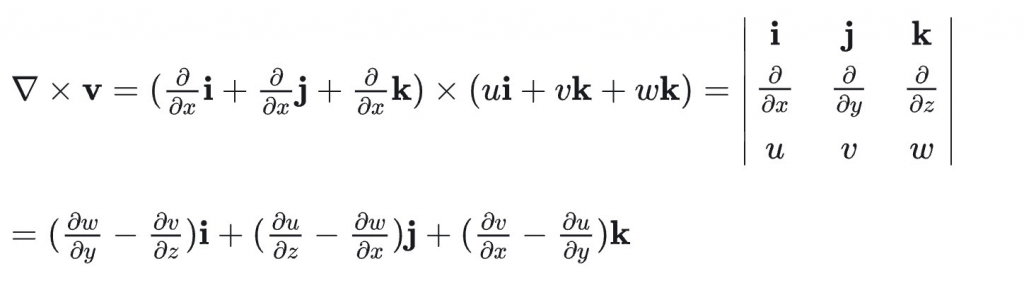
- 标量的梯度为矢量,因此对该矢量可以继续求散度,从而引入拉普拉斯算子∇2 :
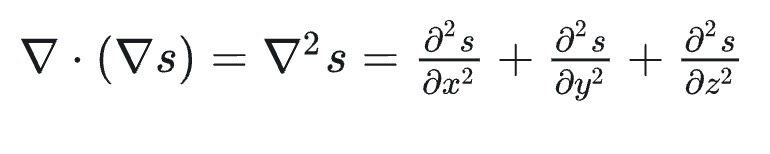
- 矢量的散度为标量,因此对该标量可以继续求梯度:
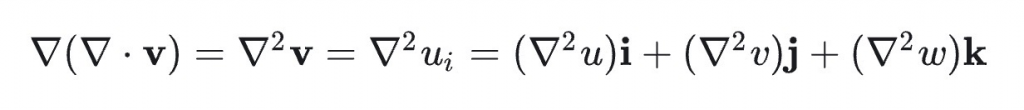
拉普拉斯算子对标量的运算结果为标量、对矢量的运算结果为矢量。
举例:
电势场的梯度是电场强度,电场强度的的散度等于q/ε,高斯定理



xuenhua’s 站点
0、哈密顿算子∇
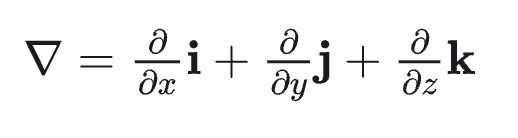
1、梯度(Gradient)是矢量,也是法向量
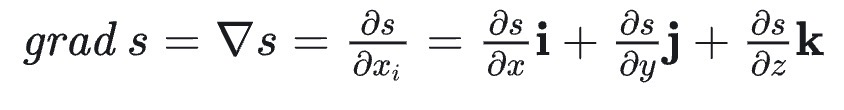
2、散度(Divergence)是标量
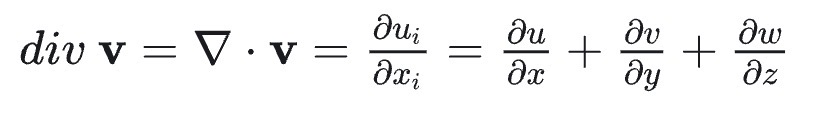
3、旋度(Curl)是向量
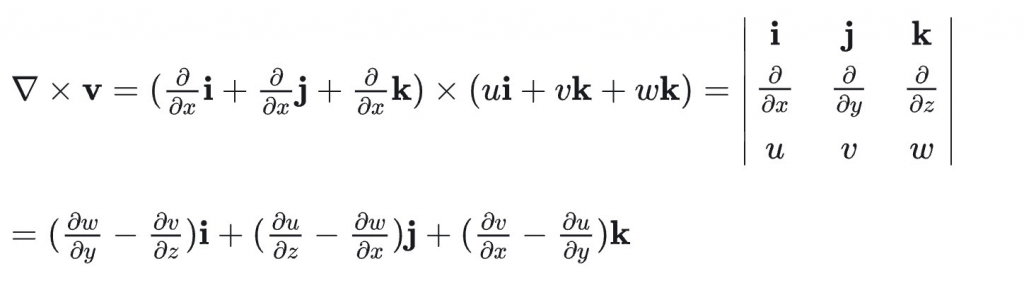
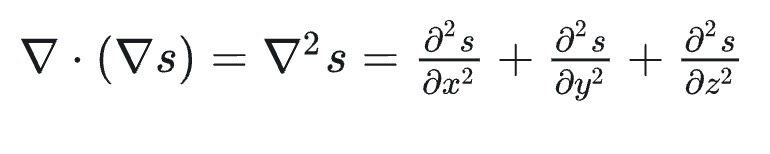
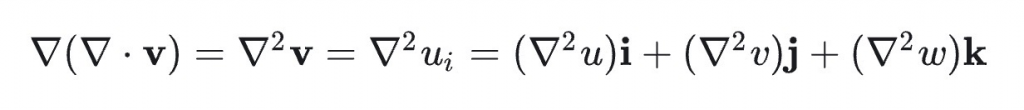
拉普拉斯算子对标量的运算结果为标量、对矢量的运算结果为矢量。
举例:
电势场的梯度是电场强度,电场强度的的散度等于q/ε,高斯定理


观察各个项,行和列按的顺序排列成表格,每个格子内为行列相乘的项,平方项恰在对角线位置,其他项放在对角线上三角区域,可以得到下面方阵: 如果把像 这样的2倍的系数沿着对角线对称的位置拆分放置,即,那么可以得到下面的样子:
继续阅读“二次型与矩阵对应关系”一元n次方程 的根为,其中。 那么(1)式可以写成下面的形式:
将其展开,并观察多项式系数,的系数: 常数项:
比较常数项和的系数,可以得到:
这就是一元n次方程的韦达公式。
在初中我们就学过很多种直线的表示
继续阅读“直线与平面的向量表示”一般式: 不能同时为零;
斜截式: ,其中 是斜率(slope),表示直线与x轴正方向夹角的正切值, 是纵截距(y-intercept,截距可以是负值),表示直线与y轴的交点的纵坐标;
点斜率: ,其中 表示直线上一点, 表示直线斜率;
截距式: ,其中 分别表示直线与x轴和y轴的截距,也就是与x轴交点的横坐标和与y轴交点的纵坐标;
两点式: ,其中 表示直线上两点坐标;
GDI+ 提供用于存储和操作图像的 Image 和 Bitmap 类。 Image 和 Bitmap 对象用一个 32 位数字存储每个像素的颜色:红、绿、蓝和 Alpha 各 8 位。 这四个分量的值都是 0 到 255,其中 0 表示没有亮度,255 表示最大亮度。 alpha 分量指定颜色的透明度:0 表示完全透明,255 表示完全不透明。
颜色矢量采用 4 元组形式(红色、绿色、蓝色、alpha)。 例如,颜色矢量 (0, 255, 0, 255) 表示一种没有红色和蓝色但绿色达到最大亮度的不透明颜色。
表示颜色的另一种惯例是用数字 1 表示亮度达到最大。 通过使用这种约定,上一段中描述的颜色将可以由矢量 (0, 1, 0, 1) 表示。 在执行颜色变换时,GDI+ 遵循使用 1 为最大亮度的惯例。
可通过用 4×4 矩阵乘以这些颜色矢量将线性变换(旋转和缩放等)应用到颜色矢量中。 但是,您不能使用 4×4 矩阵进行平移(非线性)。 如果在每个颜色矢量中再添加一个虚拟的第 5 坐标(例如,数字 1),则可使用 5×5 矩阵应用任何组合形式的线性变换和平移。 由线性变换组成的后跟平移的变换称为仿射变换。
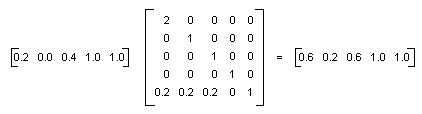
例如,假设您希望从颜色 (0.2, 0.0, 0.4, 1.0) 开始并应用下面的变换:
下面的矩阵乘法将按照列出的顺序进行这对变换。
颜色矩阵的元素按照先行后列(从 0 开始)的顺序进行索引。 例如,矩阵 M 的第五行第三列由 M[4][2] 表示。
5×5 单位矩阵(在下面的插图中显示)在对角线上为 1,在其他任何地方为 0。 如果用单位矩阵乘以颜色矢量,则颜色矢量不会发生改变。 形成颜色变换矩阵的一种简便方法是从单位矩阵开始,然后进行较小的改动以产生所需的变换。

有关矩阵和变换的更详细的讨论,请参见坐标系统和变形。
示例
下面的示例采用一个使用一种颜色 (0.2, 0.0, 0.4, 1.0) 的图像,并应用上一段中描述的变换。
下面的插图在左侧显示原来的图像,在右侧显示变换后的图像。

下面示例中的代码使用以下步骤进行重新着色:
C#
Image image = new Bitmap(“InputColor.bmp”);
ImageAttributes imageAttributes = new ImageAttributes();
int width = image.Width;
int height = image.Height;
float[][] colorMatrixElements = {
new float[] {2, 0, 0, 0, 0}, // red scaling factor of 2
new float[] {0, 1, 0, 0, 0}, // green scaling factor of 1
new float[] {0, 0, 1, 0, 0}, // blue scaling factor of 1
new float[] {0, 0, 0, 1, 0}, // alpha scaling factor of 1
new float[] {.2f, .2f, .2f, 0, 1}}; // three translations of 0.2
ColorMatrix colorMatrix = new ColorMatrix(colorMatrixElements);
imageAttributes.SetColorMatrix(
colorMatrix,
ColorMatrixFlag.Default,
ColorAdjustType.Bitmap);
e.Graphics.DrawImage(image, 10, 10);
e.Graphics.DrawImage(
image,
new Rectangle(120, 10, width, height), // destination rectangle
0, 0, // upper-left corner of source rectangle
width, // width of source rectangle
height, // height of source rectangle
GraphicsUnit.Pixel,
imageAttributes);
编译代码
前面的示例是为使用 Windows 窗体而设计的,它需要 Paint 事件处理程序的参数 PaintEventArgse。