直线与平面的向量表示

在初中我们就学过很多种直线的表示

一般式： $Ax+By+C=0$ $A,B$不能同时为零；
斜截式： $y = kx + b$ ,其中 $k$ 是斜率(slope)，表示直线与x轴正方向夹角的正切值，$b$ 是纵截距(y-intercept,截距可以是负值)，表示直线与y轴的交点的纵坐标；
点斜率： $y – y_{1} = k(x – x_{1})$,其中 $(x_{1},y_{1})$ 表示直线上一点， $k$表示直线斜率；
截距式： $\frac{x}{a} + \frac{y}{b} = 1$,其中 $a,b$分别表示直线与x轴和y轴的截距，也就是与x轴交点的横坐标和与y轴交点的纵坐标；
两点式： $\frac{x – x_{1}}{x_{2} – x_{1}} = \frac{y – y_{1}}{y_{2} – y_{1}}$，其中 $(x_{1},y_{1}),(x_{2},y_{2})$ 表示直线上两点坐标；

上述这些，我们学的都是在二维平面中的直线表示，如果到三维空间中直线该如何表示呢？那么进一步一个平面又该如何表示呢？

那么本文就来介绍一下直线与平面的向量表示。

---

一、直线的向量表示

已知直线上点 $A$和直线的的方向向量 $\overset{\rightarrow}{b}$ ,根据向量的加法运算就可以把直线上任意一点 $R$都可以表示出来。

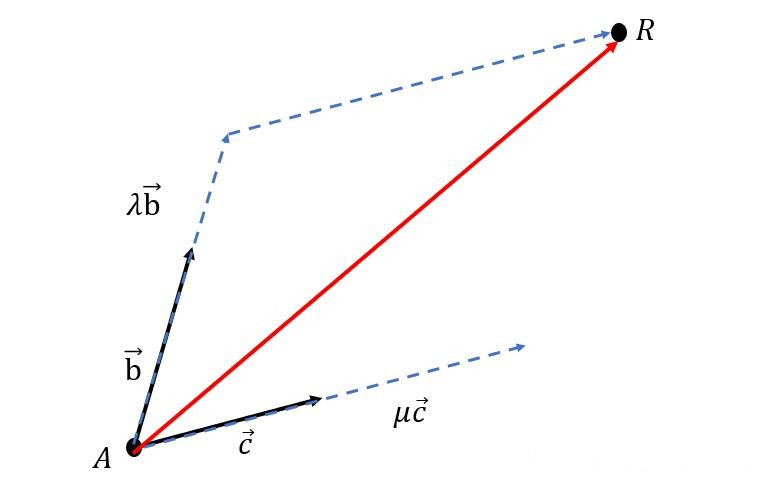
因为$\overset{\rightarrow}{OR} = \overset{\rightarrow}{OA} + \overset{\rightarrow}{AR}$ , $\overset{\rightarrow}{AR} = \lambda\overset{\rightarrow}{b}$ ，

所以，$\overset{\rightarrow}{OR} = \overset{\rightarrow}{OA} + \lambda\overset{\rightarrow}{b}$

这可以理解为直线上任意一点都可以由直线上一已知点按照方向向量平移得到。根据上述原理我们可以到直线在二维、三维情况下的向量表示。

（1）二维直线向量表示

$\left( \begin{array}{l} x \\ y \\ \end{array} \right) = \left( \begin{array}{l} x_{0} \\ y_{0} \\ \end{array} \right) + \lambda\left( \begin{array}{l} b_{1} \\ b_{2} \\ \end{array} \right)$

其中 $\left( \begin{array}{l} x_{0} \\ y_{0} \\ \end{array} \right)$是直线上点坐标， $\left( \begin{array}{l} b_{1} \\ b_{2} \\ \end{array} \right)$是方向向量， $\lambda$是参数。

根据上述式子很容易得到直线的参数方程：

$\left\{ \begin{array}{l} {x = x_{0} + \lambda b_{1}} \\ {y = y_{0} + \lambda b_{2}} \\ \end{array} \right.$ ，

也把 $\lambda$ 消去得到直线的笛卡尔坐标形式：

$$\frac{x – x_{0}}{b_{1}} = \frac{y – y_{0}}{b_{2}}$$

（2）三维直线向量表示

$\left( \begin{array}{l} x \\ y \\ z \\ \end{array} \right) = \left( \begin{array}{l} x_{0} \\ y_{0} \\ z_{0} \\ \end{array} \right) + \lambda\left( \begin{array}{l} b_{1} \\ b_{2} \\ b_{3} \\ \end{array} \right)$

其中 $\left( \begin{array}{l} x_{0} \\ y_{0} \\ z_{0} \\ \end{array} \right)$是直线上一点， $\left( \begin{array}{l} b_{1} \\ b_{2} \\ b_{3} \\ \end{array} \right)$是方向向量。

同理可以到直线的参数方程：

$\left\{ \begin{array}{l} {x = x_{0} + \lambda b_{1}} \\ {y = y_{0} + \lambda b_{2}} \\ {z = z_{0} + \lambda b_{3}} \\ \end{array}\right.$

笛卡尔坐标形式:

$$\frac{x – x_{0}}{b_{1}} = \frac{y – y_{0}}{b_{2}} = \frac{z – z_{0}}{b_{3}}$$

比如给一直线方程 $\frac{x – 1}{2} = \frac{3 + y}{3} = z$，

那么可以知道该直线过 $(1,-3,0)$ ，且方向向量为 $\left( \begin{array}{l} 2 \\ 3 \\ 1 \\ \end{array} \right)$ 。

---

二、平面的向量表示

平面的向量表示有两种不同的方法:一种是利用向量的合成，一种是利用法向量。

（1）向量的合成

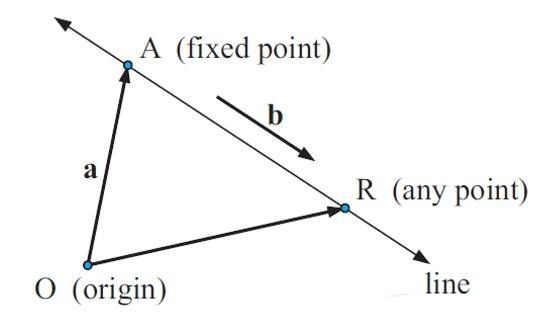
如果已知平面内一点 $A\left( a_{1},a_{2},a_{3} \right)$

和两个不平行的向量 $\overset{\rightarrow}{b} = \left( \begin{array}{l} b_{1} \\ b_{2} \\ b_{3} \\ \end{array} \right)$ 和 $\overset{\rightarrow}{c} = \left( \begin{array}{l} c_{1} \\ c_{2} \\ c_{3} \\ \end{array} \right)$ ，那么平面内任意一点 $R$ 都存在常数$\lambda,\mu$使得下式成立：

$\overset{\rightarrow}{AR} = \lambda\overset{\rightarrow}{b} + \mu\overset{\rightarrow}{c}$ ,

又因为 $\overset{\rightarrow}{OR} = \overset{\rightarrow}{OA} + \lambda\overset{\rightarrow}{b} + \mu\overset{\rightarrow}{c}$ ,即：

$\left( \begin{array}{l} x \\ y \\ z \\ \end{array} \right) = \left( \begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \\ \end{array} \right) + \lambda\left( \begin{array}{l} b_{1} \\ b_{2} \\ b_{3} \\ \end{array} \right) + \mu\left( \begin{array}{l} c_{1} \\ c_{2} \\ c_{3} \\ \end{array} \right)$

我们二维的平面直角坐标系也可以看成是两个相互垂直的基向量加减运算得到：

$\left( \begin{array}{l} x \\ y \\ z \\ \end{array} \right) = \left( \begin{array}{l} 0 \\ 0 \\ 0 \\ \end{array} \right) + \lambda\left( \begin{array}{l} 1 \\ 0 \\ 0 \\ \end{array} \right) + \mu\left( \begin{array}{l} 0 \\ 1 \\ 0 \\ \end{array} \right)$

（2）法向量

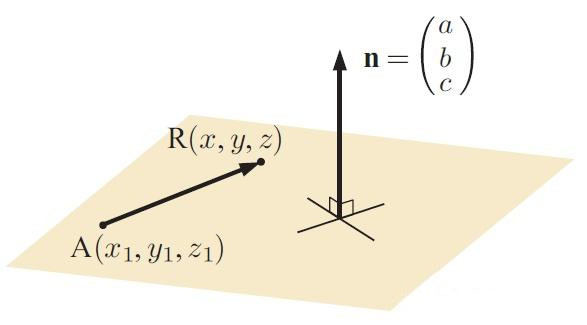
把与平面中任意向量都相互垂直的向量称为法向量。如果已知平面上一点 $A\left( x_{1},y_{1},z_{1} \right)$ 和平面的法向量 $\overset{\rightarrow}{n} = \left( \begin{array}{l} a \\ b \\ c \\ \end{array} \right)$ ，那么点 $A$ 和平面内任意一点 $R(x,y,z)$ 所构成的向量 $\overset{\rightarrow}{AR}$ 与法向量垂直可得：

$\overset{\rightarrow}{n} \bullet \overset{\rightarrow}{AR} = 0$

$\left( \begin{array}{l} a \\ b \\ c \\ \end{array} \right) \cdot \left( \begin{array}{l} {x – x_{1}} \\ {y – y_{1}} \\ {z – z_{1}} \\ \end{array} \right) = 0$

所以，$a\left( x – x_{1} \right) + b\left( y – y_{1} \right) + c\left( z – z_{1} \right) = 0$

得到平面的一般方程：

$ax + by + cz = ax_{1} + by_{1} + cz_{1}$ .

因此，型如$Ax + By + Cz = D$ 的都是平面方程，且 $\left( \begin{array}{l} A \\ B \\ C \\ \end{array} \right)$ 是该平面的法向量。

比如给一平面方程 $2x + 4y + z = 1$，那么该平面的法向量为 $\left( \begin{array}{l} 2 \\ 4 \\ 1 \\ \end{array} \right)$ ；那么如果平面方程为 $3x + 5y = 1$ 其法向量为多少呢？

其法向量为$\left( \begin{array}{l} 3 \\ 5 \\ 0 \\ \end{array} \right)$ 。

至此，直线和平面的向量表示都已经介绍完毕，在此基础上向量还有两个重要的应用：距离与夹角。