基本参数
地球公转周期 365.2564 天
月球公转周期 27.32166 天
月球轨道面与地球轨道面交角
地球和月球都是椭圆轨道,但是考虑离心率都很小,可以近似为圆形。
计算思路
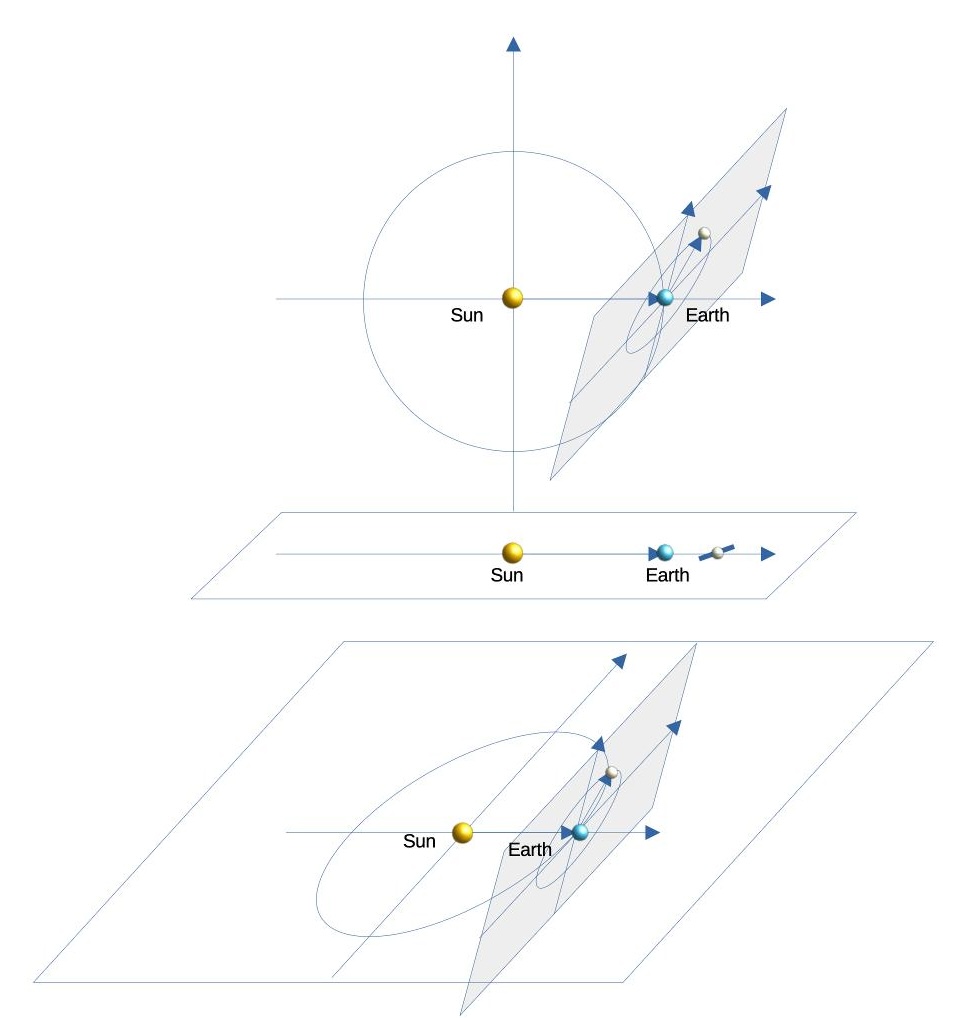
计算月食或者日食即计算向量 和 的夹角如果接近0,即太阳、地球、月球一线月食发生。类似,若夹角180度,即日食发生。

xuenhua’s 站点
地球公转周期 365.2564 天
月球公转周期 27.32166 天
月球轨道面与地球轨道面交角
地球和月球都是椭圆轨道,但是考虑离心率都很小,可以近似为圆形。

计算月食或者日食即计算向量 和 的夹角如果接近0,即太阳、地球、月球一线月食发生。类似,若夹角180度,即日食发生。
我们经常收到银行的贷款推销,有的利息较高,我们通常就直接拒绝了,但是有些看似利息较低甚至可以“赚差价”的,没有仔细计算就接受了。如果仔细计算,就会发现其实中了圈套。
真实案例:
贷款分12期还款,贷款10000的话,每月还款848.333(等额本息),总计还款10180,年化利率1.8%?虽然1年期存款利率目前已经进入1时代,但是有些小银行或者理财产品可以做到2左右。按2%的平均利息水平粗略一算,10000块存起来可以赚200利息,贷款利息180,还能赚20块钱。聪明的读者,这样算对吗?能赚到利息差价吗?
乍一看,好像是赚了20块钱,但实际上赔了73块。下面我给大家详细算一下。
继续阅读“银行推销的“低息”贷款到底划算吗?”0、哈密顿算子∇
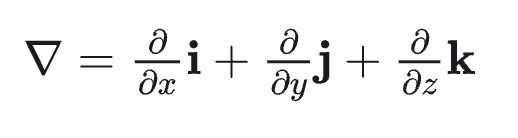
1、梯度(Gradient)是矢量,也是法向量
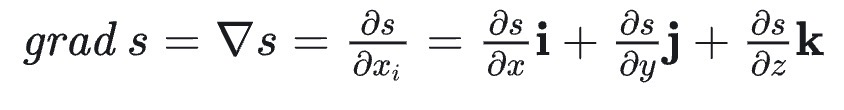
2、散度(Divergence)是标量
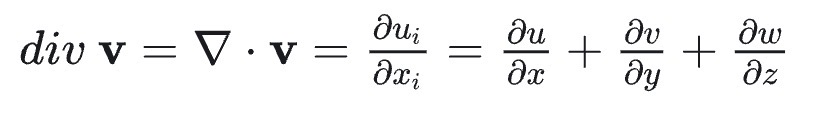
3、旋度(Curl)是向量
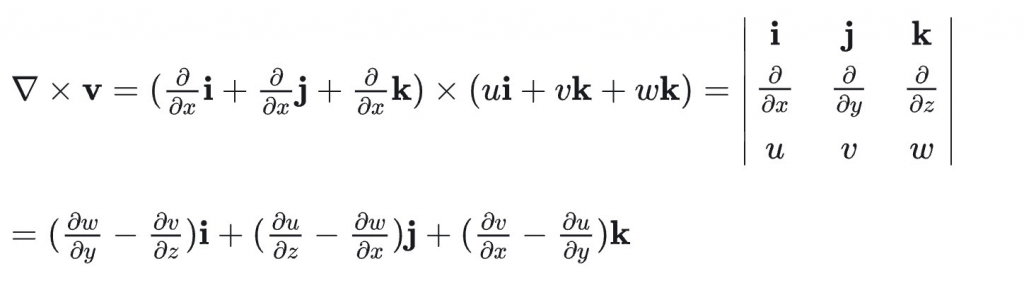
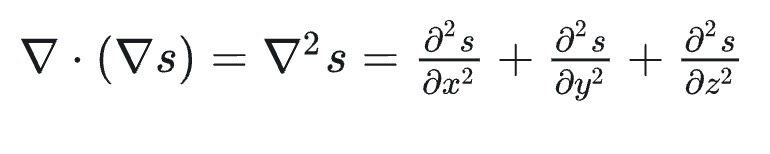
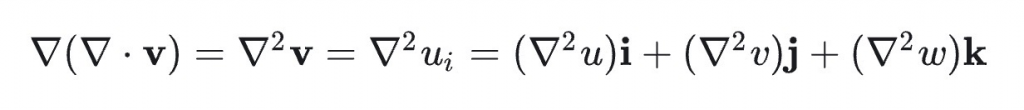
拉普拉斯算子对标量的运算结果为标量、对矢量的运算结果为矢量。
举例:
电势场的梯度是电场强度,电场强度的的散度等于q/ε,高斯定理


如遇网络问题无法下载,可以尝试国内镜像,网址把github改为gitee,其它不变
数论-陈景润.pdf观察各个项,行和列按的顺序排列成表格,每个格子内为行列相乘的项,平方项恰在对角线位置,其他项放在对角线上三角区域,可以得到下面方阵: 如果把像 这样的2倍的系数沿着对角线对称的位置拆分放置,即,那么可以得到下面的样子:
继续阅读“二次型与矩阵对应关系”