§7-1 电子波与电磁透镜
一、光学显微镜的分辨率极限
物体上的光点通过显微镜成像时,在象平面上得到的是一个中心最亮、周围常有明暗相间同心圆环的圆斑,即埃利(Airy)斑。若样品上有两个光点A、B通过显微镜成像,在象平面上会产生两个埃利斑A′、B′,如图7-1所示。如果这两个埃利斑相互靠近至两者中心间距等于第一暗环半径R0,此时两个光斑强度峰间的强度谷值比强度峰值低19%(设强度峰值为100%),这个反差值是人眼能分辨出两个物点像的临界值。通常把两埃利斑中心间距等于R0时,样品上对应的两个物点间的距离△r0定义为显微镜能分辨的最小距离,即显微镜的分辨率,它决定了显微镜分辨试样细节的程度。
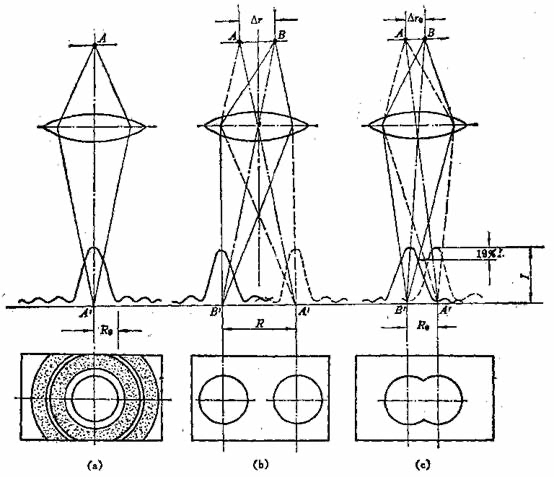
(a) 一物点的埃利斑像及其光强度分布 (b)相距比较远的两物点的埃利斑像 (c) 相距比较近的两物点的埃利斑及其光强度叠加
图7-1 光的衍射和显微镜的分辨率
由衍射效应所决定的分辨率在理论上可以采用Rayleigh公式计算:
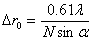
(7-1)
式中λ为照明光源的波长,N为介质的相对折射系数,α为显微镜的孔径半角。
可见光的波长大致在400~800nm之间,最佳情况下光学显微镜的分辨率最高可达0.2μm。
由式(7-1)可以看出,提高显微镜分辨率的最有效方法是采用短波长的照明光源。x射线和γ射线的波长都很短,但至今还无法使之有效地改变方向、折射和聚焦成像。1924年,德布罗意(De Broglie)发现电子波的波长比可见光的波长短十万倍;1926年,布什(Busch)指出轴对称非均匀磁场能使电子波聚焦。这些理论的出现,表明可以采用电子波作为显微镜的光源。在1933年鲁斯卡(Ruska)等人设计并制造了世界上第一台透射电子显微镜。
二、电子波的波长
电子显微镜的照明光源是电子波。电子波的波长取决于加速电压和电子的质量,即

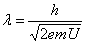
(7-2)
式中 h为普朗克常数,m为电子的质量;e为电子所带的电荷,U为加速电压。
如果电子速度较低,则它的质量和静止质量相近,即m≈m0。如果加速电压很高,使电子具有极高的速度,则必须经过相对论校正,此时
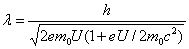
(7-3)
表7-1是根据式(7-4)计算出的不同加速电压下电子波的波长。
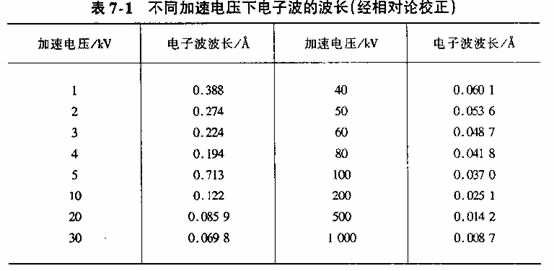
在常用的100~200kV加速电压下,电子波的波长比可见光小5个数量级。
问题:电子束的波长比可见光小5个数量级,透射电子显微镜的分辨率理论上可否达到0.002nm?
三、静电透镜与磁透镜
1. 静电透镜
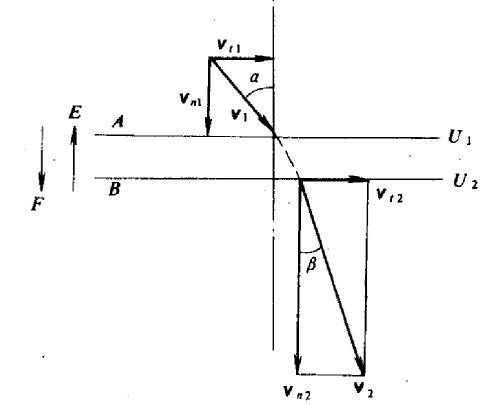
图7-2 电子束在电场作用下折射
电子在静电场中由于受到电场力的作用,将使运动方向发生偏转,如图7-2所示。
我们把静电场的等位面做成凸透镜形状,那么平行电子束也将会聚在一个焦点上。图7-3是静电透镜的示意图,其中U1<U2,相应的电力线方向如图所示。在垂直于电力线的方向画出等位面,其形状与凸透镜相似。当平行的电子束从低向高入射时,就会在圆筒轴线的某一点上聚焦。
早期的电子显微镜中曾使用过静电透镜。由于静电透镜需要很强的电场,常在镜筒内产生弧光放电和电击穿,低真空度情况下尤为严重。静电透镜焦距不能很短,因而不能很好地矫正球差。现在制造的透射电子显微镜,静电透镜仅用于使电子枪中的阴极发射出的电子会聚成很细的电子束,而不用来成像。

图7-3 静电透镜示意图
2.磁透镜
电子在磁场中运动时也会产生偏折,图7-4为磁透镜的聚焦原理示意图。通电的短线圈就是一个简单的磁透镜,它能造成一种不均匀分布的磁场,结果使电子做如图7-4所示的圆锥螺旋近轴运动。一束平行于主轴的入射电子通过电磁透镜将最终会聚于轴线上一点(即焦点)。
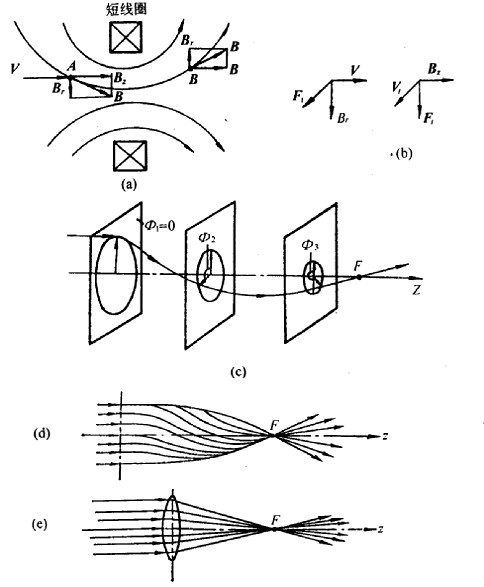
图7-4 电磁透镜的聚焦原理示意图
图7-5为一种带有铁壳的电磁透镜示意图。导线外围的磁力线都在铁壳中通过,由于在软磁壳的内侧开有一道环状的窄缝,可以减小磁场的广延度,使大量磁力线集中在缝隙附近的狭小区域内,增强了磁场的强度。为了进一步缩小磁场轴向宽度,还可以在环状间隙两边,接出一对顶端成圆锥状的极靴,如图7-6所示。带有极靴的电磁透镜可使有效磁场集中在沿透镜轴向几毫米的范围内。
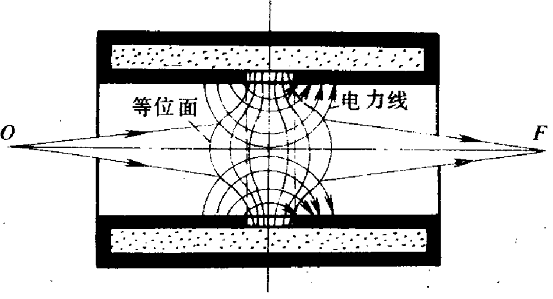
图7-5 带有软磁壳的磁透镜示意图
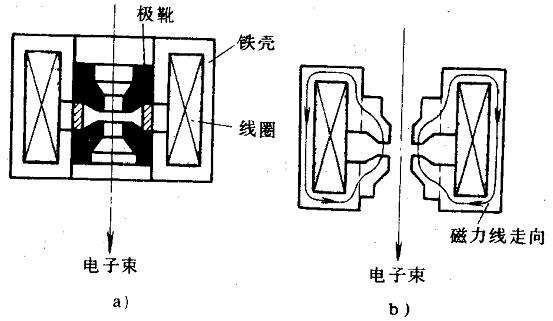
(a)结构图 (b)磁力线在极靴中行进路线
图7-6 带有极靴的磁透镜
3. 磁透镜与光学透镜的比较
光学透镜成像时,物距L1、象距L2、焦距f三者之间满足下述关系式:

(7-4)
由于光学透镜的焦距f是不能改变的,要满足成像条件,必须同时改变L1和L2。
与光学透镜相似,电磁透镜成像时也必须满足式(7-4)。但磁透镜的焦距可以通过改变线圈中通过电流的大小来调节。采用磁透镜成像时,可以在固定L1的情况下,改变f和L2来满足成像条件;也可以保持L2不变,改变f和L1来满足成像条件

