卷积神经网络是一种前馈神经网络,用于图片分类的卷积网络一般包含两部分:卷积部分和全链接部分。
卷积部分将传统的卷积操作中卷积核的值当成了训练的对象,并加入了池化层,激活层,专门用来提取图片特征。全链接部分就是普通的神经网络,前面以图片特征为输入,后面加上softmax层来输出每个类的概率。
卷积神经网络推理时只有前馈过程;在训练时多使用了一个后馈过程来更新权重,达到学习的目的。
前馈过程:
图片预处理
进入运算之前,图片先是从各种格式,JPG,PNG,BMP转换成为一个张量(Tensor)。张量的维度一般是(图片高,图片宽,层数),层数一般为(R,G,B)三层。
由于全链接层的输入大小是固定的,通常改变图片尺寸,比如长宽resize成224 * 224。
(如果你用mini batch来跑,一次性输入一个batch,维度会变成(batch大小,图片高,图片宽,层数))
然后进行卷积运算
概念:padding
卷积运算对于最边缘的像素不是太公平,因为中间的像素都能被更多卷积运算运用到,比重更大,所以可以在外面填充一圈零。(类似于传统卷积运算的边缘效应)
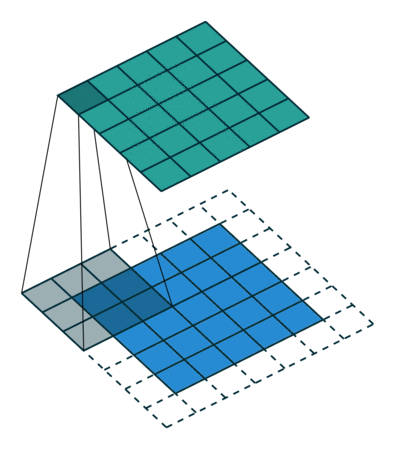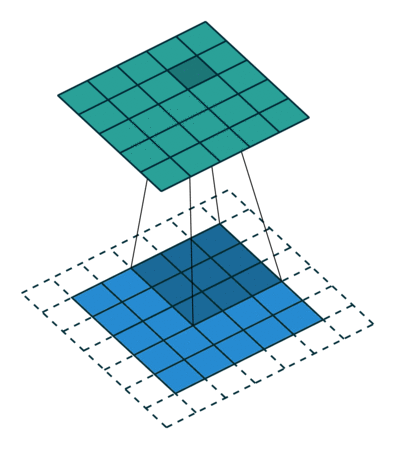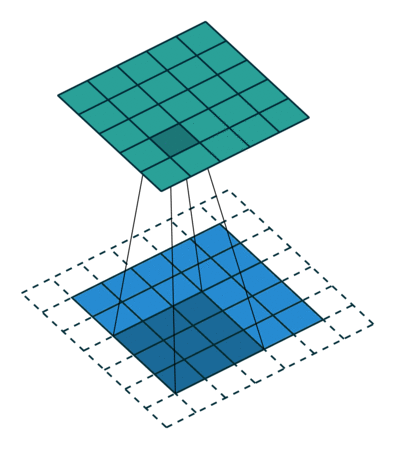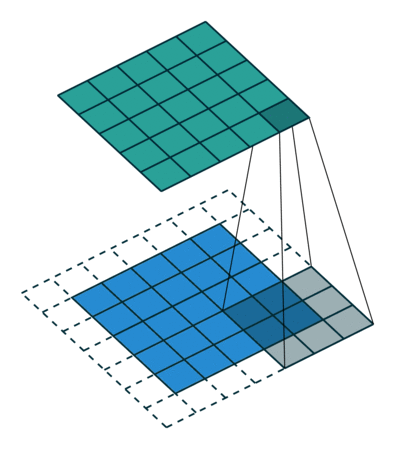
下面是在同样尺寸的输入,卷积核3*3,stride为(1,1)情况下,padding分别为1,2的时候:
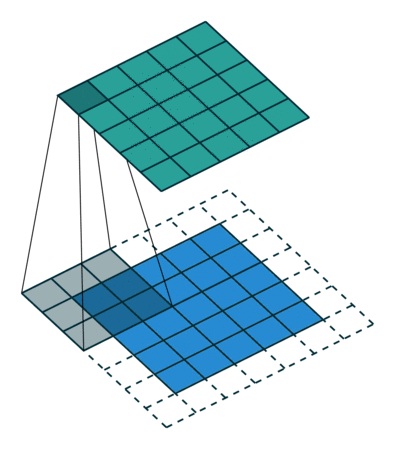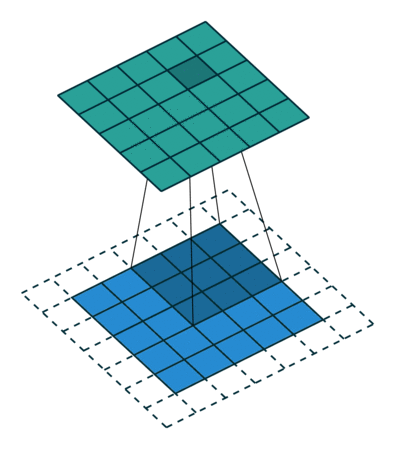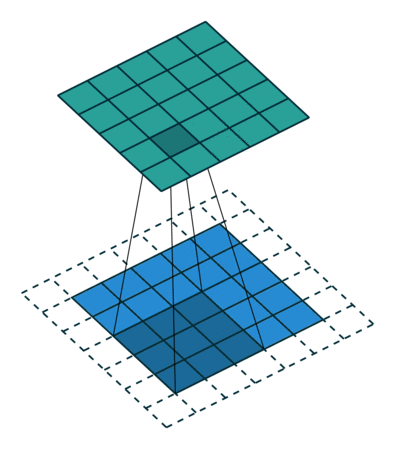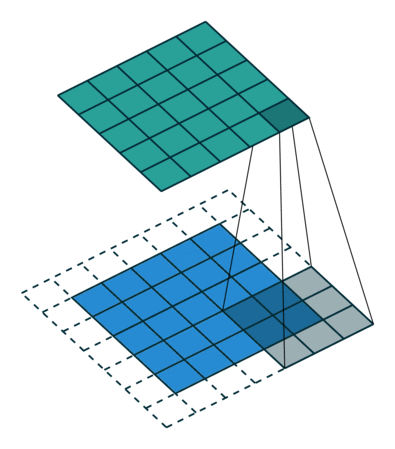
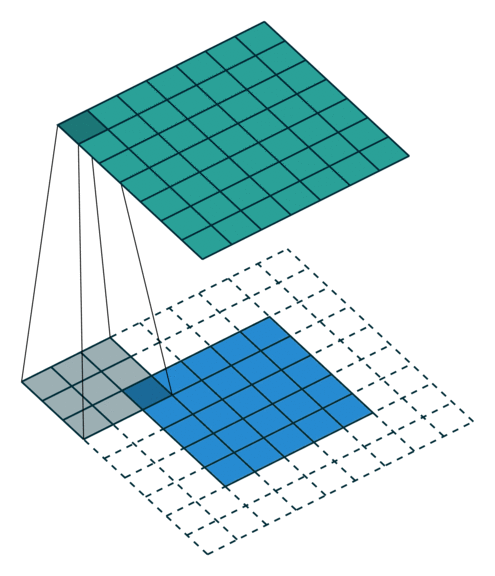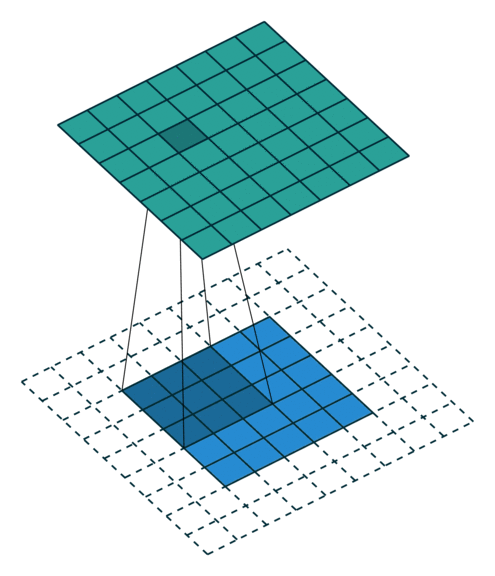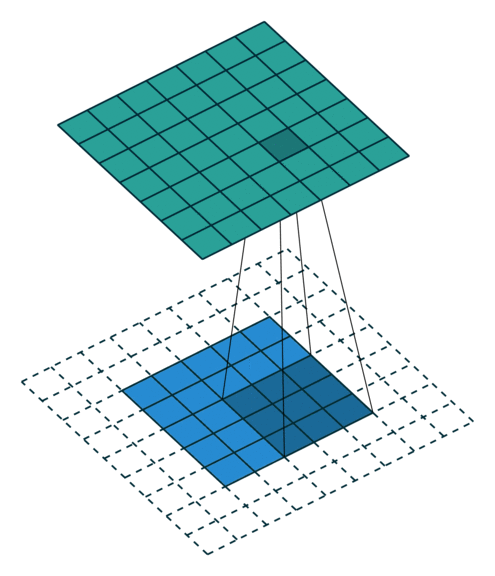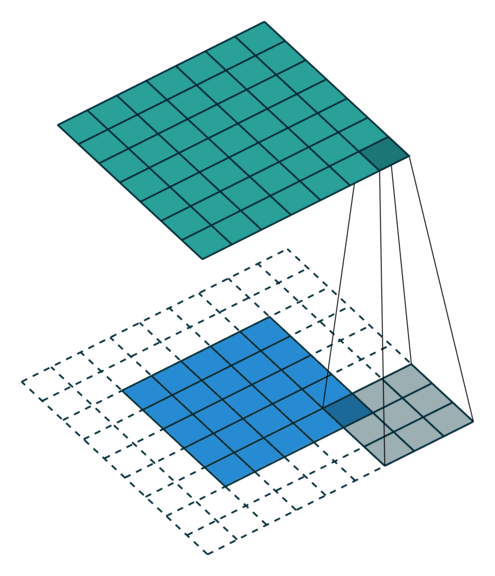
左边这个由于padding的存在,卷积操作的输入输出尺寸相同,我们叫same padding。
概念:stride
就是每次卷积操作每一次移动的步数,下面是在同样的3*3卷积核,padding为1的情况下,stride分别为(1,1)和(2,2)的时候:

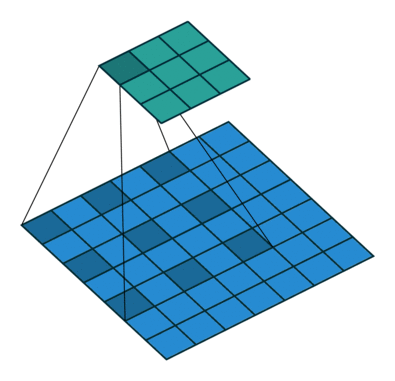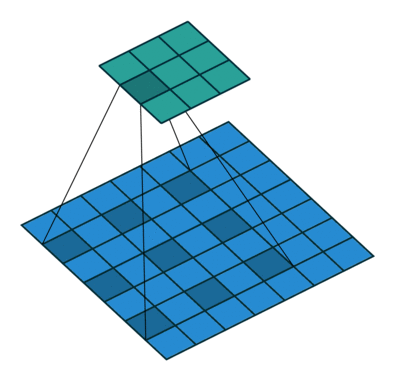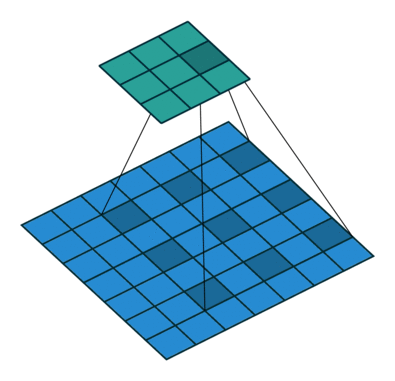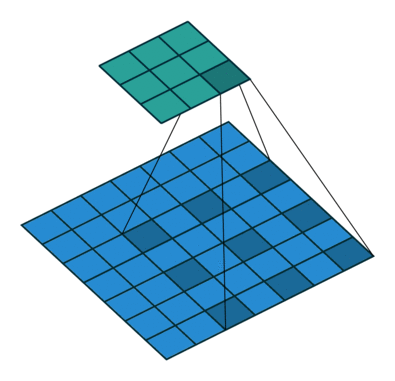
RGB的卷积核操作:
可以看到,针对RGB的卷积核其实是三层的,经过卷积运算后,rgb三层图片变成了一层。
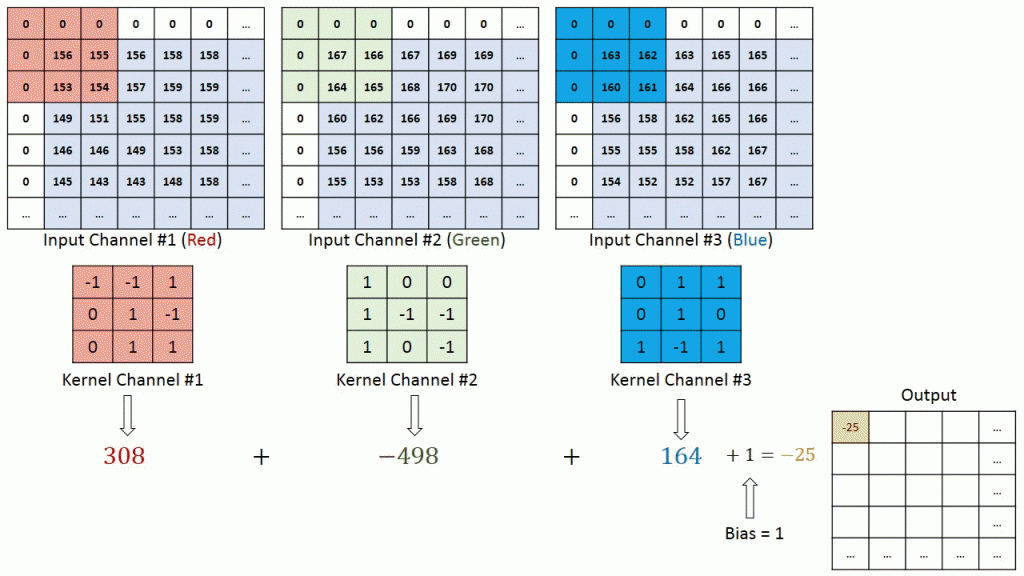
可以预见如果中间的卷积核的输入是十层,那我们的每个卷积核也要相应的变成十层,每个卷积的参数数量也要相应增加。
两个卷积核的情况下:
简单的讲,我们使用了几个卷积核(filter),下面就有几层。

激活函数
常见的激活函数有relu,sigmoid和tanh等,卷积层常用relu。
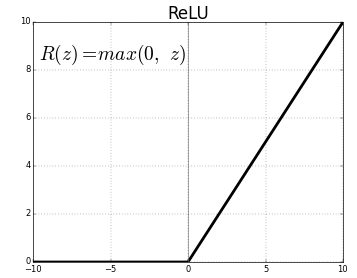
Relu对正数值维持一个线性的操作,负数值会被置零,即不会被更新。
卷积操作+激活函数 代码
卷积操作后面一般都会跟着非线形的激活函数,不然它卷积多少次都是个线形函数。
这里我们使用了32个3×3的卷积核,stride为(1,1),same padding,激活函数使用了relu。
可以预见,我们这个卷积层的输出为32层,每层的长宽与前一层一样,经过了relu层所有的值都变成>=0。
conv1 = tf.layers.conv2d(
inputs=prevous_layer,
filters=32,
kernel_size=[3, 3],
strides=(1, 1),
padding="same",
activation=tf.nn.relu)池化层(Pooling Layer)
使用池化层在保留主要的特征同时减少参数量,以减少下一层的计算量(降维)。也可以防止过拟合,提高模型的泛化能力。下图演示常用的Max Pooling
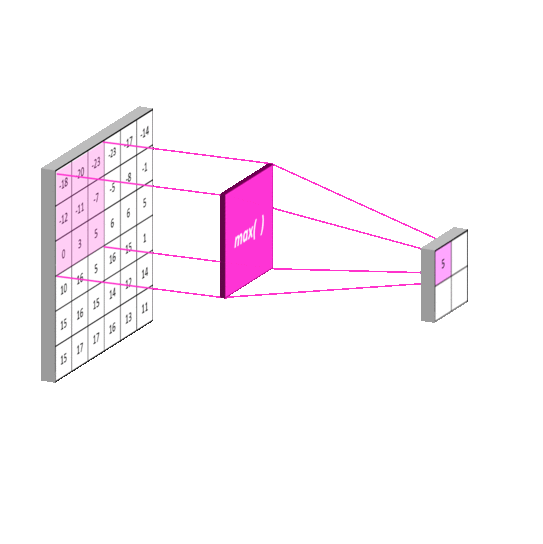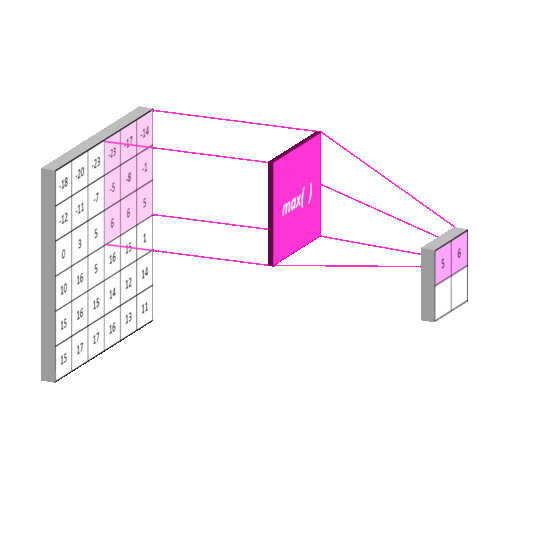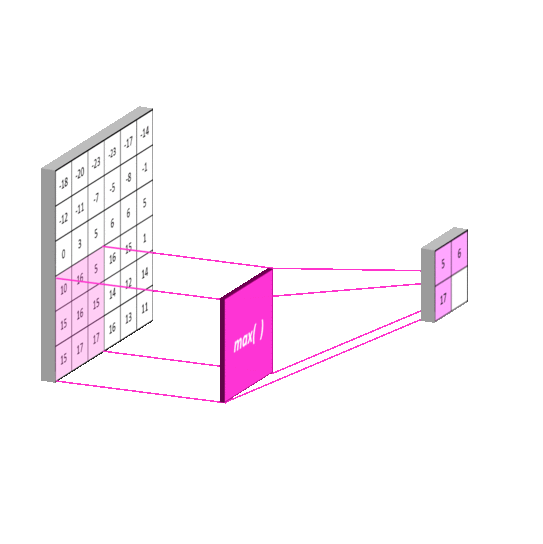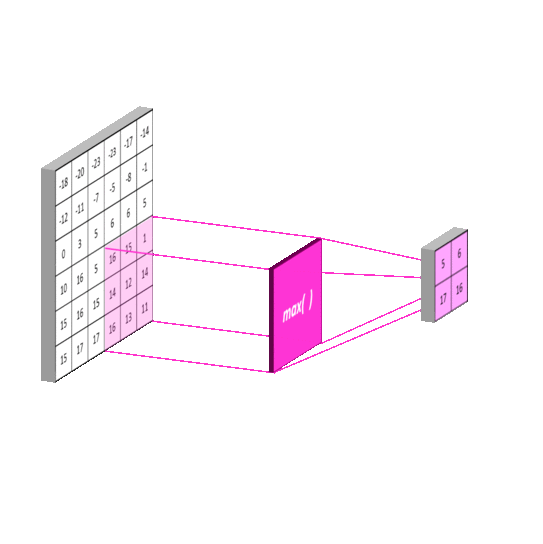
特殊情况下,如果使用SSP(Spatial Pyramid Pooling)的话,可以无视上一层的长宽,得到固定长宽的输出。
Ps. 现在也流行使用空洞卷积进行降维。
卷积层后面是Flatten层
做完卷积运算,结果是好几层特征图像,图像的特征提取到此结束。然后我们使用Flatten将它们reshape成一维数据,以便作为后面全链接层的输入。(Ps.其实可以把后面的全链接层换成SVM啊 决策树啊)(Ps.特征的位置信息其实还是保留在每个特征的排列顺序上面的)。
Flatten层在这里的作用,是连接卷积层和全链接层。
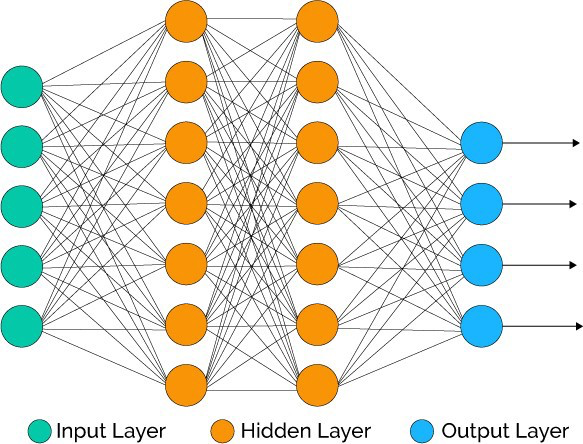
然后是全连接层
一般是普通的全链接神经网络,输入为Flatten之后的一维的图片特征,输出层一般是Sigmoid层。
然后是softmax层(分类问题)
将全链接层的输出,进行softmax运算,得到每个类的概率。
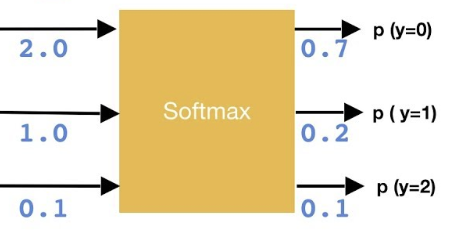
由这个等式可以看出,在二分类的时候,softmax函数其实就是sigmoid。
import numpy as np
z = [2.0, 1.0, 0.1]
print(np.exp(z)) # [7.3890561 2.71828183 1.10517092]
softmax = np.exp(z)/np.sum(np.exp(z))
print(softmax) # [0.65900114 0.24243297 0.09856589]然后计算 Loss值
Loss函数有很多种,可以由你自己根据目标定义。一般多分类问题我们使用cross entropy。
y’为预测结果,y为真实值,y‘与y求得cross entropy的值。
import numpy as np
Y = np.array([1, 0, 0]) # 真实类别为第一类
Y_pred1 = np.array([0.7, 0.2, 0.1]) # 预测1
Y_pred2 = np.array([0.1, 0.3, 0.6]) # 预测2
print('预测1 loss = ', np.sum(-Y * np.log(Y_pred1))) # 预测1 loss = 0.35
print('预测2 loss = ', np.sum(-Y * np.log(Y_pred2))) # 预测2 loss = 2.30后馈过程:
优化网络,改变Weights,让Loss变小
改变神经网络中的权重weights,来优化我们的Loss值,使它变小。 那么怎样优化呢 ?
让我们把整个卷积神经网络,从头到尾整个前馈过程,看成一个数学公式。变量为权重Weights,结果为Loss值。我们想要得到最小的Loss值,我们可以对这个数学公式进行求导,可是这个优化问题是个np hard问题,想简单的来个导数为零…这个等式解不出来,所以我们采用了梯度下降法。
简单的讲,对每一个变量(权重Weights)求,然后我们让这个权重按照这个值的相反方向运动,以达到减小Loss的效果。
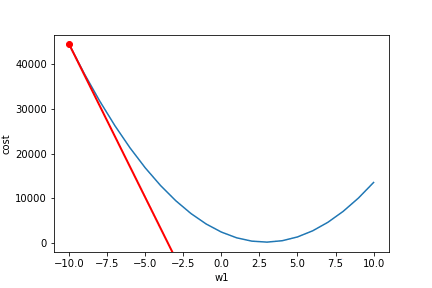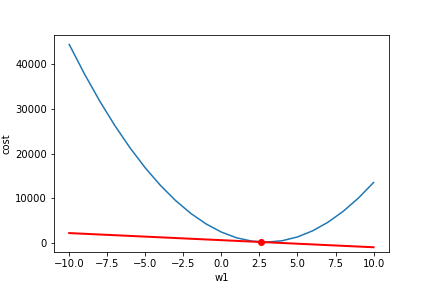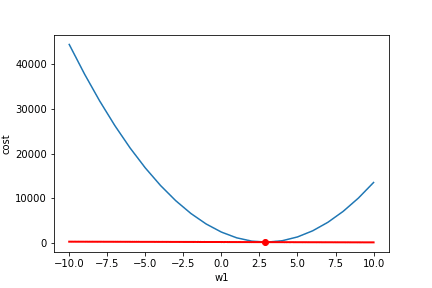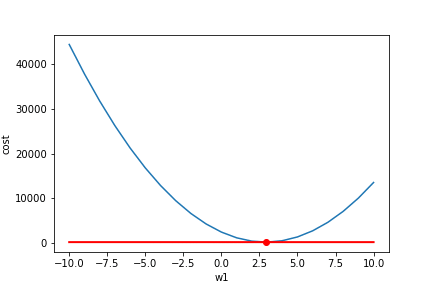
我们可以看到左边的导数值都是负的,我们就讲weight往相反方向(正方向)运动,得到最小值。
具体一点
卷积神经网络的前一层的结果,是后一层的输入。我们把每一层看成一个函数,多层神经网络其实就是很多个函数的嵌套,可以看成一个复合函数。我们高中就学过,这样的求导可以遵循链式法则(Chain Rule)。我们一层一层的求导,一步步来。
我们定义了学习率 learning rate, 每次的迭代更新每个权重w,
一个个求导太慢?我们用优化器来加速
Batch gradient descent(BGD 批量梯度下降法)
每次更新计算整个样本集的梯度,应该说这也是梯度下降算法的初衷,按照整体梯度下降的方向调整参数。可是因为每次都要计算所有数据的梯度,计算量较大,计算速度比较慢;并且计算过程中不能添加新的样本。
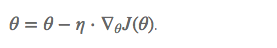
Stochastic gradient descent (SGD 随机梯度下降法)
和BGD的一次使用所有样本计算梯度相比,SGD一次只使用一个样本进行梯度更新, 这样单次的权重优化运算会比较快;并且运算过程中可以新增样本。
可是样本间的差异,还会有一些噪声数据,导致梯度下降的过程会比较曲折。
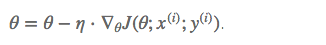
Mini-batch gradient descent (MBGD 小批量梯度下降法)
MBGD是前两种方法的折衷,每次使用一小批样本来计算。提高了梯度下降的速度都同时,又兼顾了收敛的稳定性。而且可以用到矩阵运算,充分利用GPU几千个Cuda核心进行并行运算来加速运算。
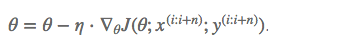
(我们现在训练使用的带有Batch Size的SGD,其实就是MBGD)
梯度下降的缺点
- 学习率的选择非常困难。如果设太小,收敛会非常缓慢;如果设太大,可能会在极小值处震荡甚至偏离。(于是我们想在离极小值远的地方采用较大学习率,在较近处采用较小学习率。)
- 可以预先制定学习率变化规则。比如,计算50轮之后,学习率减半。但是这种方法并不能得到保证,50轮之后可能依然离极小值很远。
- 需要尽量避免使Loss值收敛到优化局部最优,甚至鞍点(两者和全局最优一样,gradient都是0)
梯度下降的优化算法:
如果把多次的梯度下降看成一个时序问题,默默拿出对付时序问题的刀枪剑戟。。。
Exponentially weighted averges 指数加权平均
指数加权平均是一种非常常见的序列数据处理方式,比如预测股价。参数为β,可以用来短期(这里是局部)波动的干扰,保留长期(这里是全局)趋势。可以用来计算下一个时刻的预测值。
公式简单,只需保留上一个值,β 为之前的状态的权重,相应的1−β为当前状态的权重; β越大则越平滑,但是可能对短期的变化非常不敏感。深度学习中,一般β取值0.9左右。
Momentum 动量
想像成小球在向山下滚动的过程,中途会有很多障碍物改变它的前进方向,但是它大体上的前进方向是沿着坡向下的。在有”惯性”的情况下,它的方向会更稳定向下,速度也会更快。
我们可以看到当次的梯度的前进方向会加上上一步的前进方向乘以 γ, 一般 γ 取值 0.9 左右。
Nesterov accelerated gradient (NAG,在Momentum基础上小改,再加速)
不满足于依赖惯性,更是把当成本次移动量的预测,于是把 当成梯度下一个值的预测,并从这个值开始计算下一个位置。感觉一下子走了两步。

