发布于 由xuenhua

银行推销的“低息”贷款到底划算吗？

1. 前言

我们经常收到银行的贷款推销，有的利息较高，我们通常就直接拒绝了，但是有些看似利息较低甚至可以“赚差价”的，没有仔细计算就接受了。如果仔细计算，就会发现其实中了圈套。

真实案例：
贷款分12期还款，贷款10000的话，每月还款848.333（等额本息），总计还款10180，年化利率1.8%？虽然1年期存款利率目前已经进入1时代，但是有些小银行或者理财产品可以做到2左右。按2%的平均利息水平粗略一算，10000块存起来可以赚200利息，贷款利息180，还能赚20块钱。聪明的读者，这样算对吗？能赚到利息差价吗？

乍一看，好像是赚了20块钱，但实际上赔了73块。下面我给大家详细算一下。

2. 计算思路

比较贷款存1年的本息和每月还款总额。按照复利计算，到一年后结清贷款时我们总共的支出。然后比较二者谁大即可。

2.1 变量说明

变量 描述
N 贷款金额
m 还款期数
r 年利率，按2%
R 月利率=r/12
A 每月还款金额 848.333

2.2 存款的本息

C=N*(1+r)*1 C = N * (1+r) * 1

代入数值
C=10000*(1+0.02)*1=10200 C = 10000 * (1+0.02) * 1 = 10200

2.3 还款成本总额

计算还款总额需要考虑复利，每个月的还款复利金额为：

第1个月的还款复利为： H1=A*(1+R)m−1 H_1=A * (1+R)^{m-1}

第2个月： H2=A*(1+R)m−2 H_2=A * (1+R)^{m-2}

第3个月： H3=A*(1+R)m−3 H_3=A * (1+R)^{m-3}

第k个月： Hk=A*(1+R)m−k H_k=A * (1+R)^{m-k}

第12个月： H12=A*(1+R)m−12=A H_12=A * (1+R)^{m-12}=A

HiH_i 是等比数列，求和：

H=∑i=1mHi=A1−(1+R)m1−(1+R)=A(1+R)m−1R \begin{aligned} H &= \sum_{i=1}^{m} H_i \\ &= A \frac{1-(1+R)^m}{1-(1+R)} \\ &= A \frac{(1+R)^m-1}{R} \end{aligned}

代入数据

H=848.333*(1+0.0212)12−10.0212=10273.83 \begin{aligned} H &=848.333 * \frac{(1+\frac {0.02}{12})^{12}-1}{\frac {0.02}{12}} \\ &=10273.83 \end{aligned}

3. 贷款年化利率

3.1 计算思路

银行贷款成本等于用户还款成本。
银行贷款成本：
B=N*(1+R)m B = N*(1+R)^m

等额本息用户还款成本：

H=A(1+R)m−1R H = A \frac{(1+R)^m-1}{R}

由 $ B=H $ 可得：
A=N(1+R)m(1+R)m−1R=NR(1+R)m(1+R)m−1 \begin{aligned} A &=\frac {N(1+R)^m}{\frac{(1+R)^m-1}{R}} \\ &= \frac {NR(1+R)^m}{(1+R)^m-1} \end{aligned}

代入数据：
848.333=10000(1+R)12(1+R)12−1 848.333 = 10000 \frac {(1+R)^{12}}{(1+R)^{12}-1}

这个方程解起来有点复杂，借助数学软件：

利率应该大于0，所以只取第一象限的解。

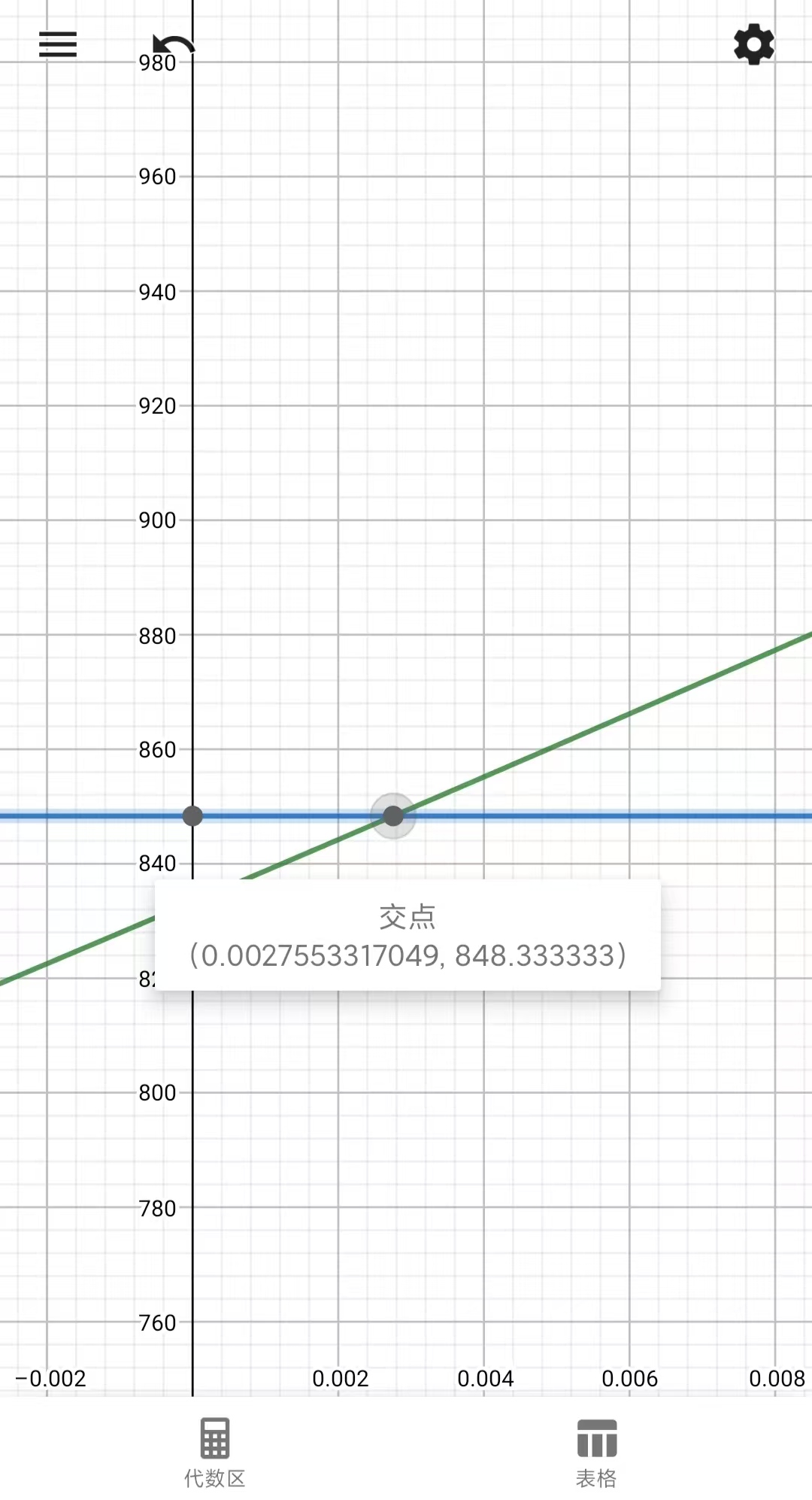
月利率为： 0.00275533
年利率为： 0.03306

4. 总结

今天的100元钱和明年的100*(1+r)100*(1+r)具有相同的价值。粗略计算时只是把每月还款额简单累加，这是不对的。还给银行的钱如果我们存银行一样可以获得利息，所以还款的成本不能简单累加，还需要计算它们的利息。

银行就是以看起来好像利息不高的方式，诱惑客户贷款，客户一般很少去精确计算还款成本，因此上当。看似年化利率只有1.8%，但是实际年化利率却高达3.3%。不仅不能赚取 0.2% 利率差价，还要赔 0.73%！